众所周知,数学猜想具有一定的科学性和很大程度的假定性,这种假定性命题是否正确,尚需通过验证和论证。科学界认为,著名数学猜想对于科学发展,尤其是数学进步的作用巨大的;在这些著名的数学难题中,数论方面的问题占据绝大多数。下面简要介绍几个著名数学猜想。
数学猜想通常由前提和结论两部分组成。它以已有的部分事实和正确的数学知识(公理、定理、公式等)为前提,以在前提的基础上作出的假定性的判断为结论。它可分为存在型猜想(如“费马猜想”),状态型猜想(如“庞加莱猜想”),关系型猜想(如“哥德巴赫猜想”),方法型猜想(如“四色问题”)等。
一、费马猜想
古希腊数学家丢番图所著的《算术》一书中,收录了一个不定方程
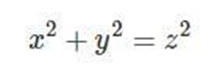
丢番图给出了该不定方程的一组正整数解
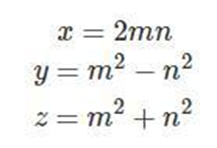
其中m>n是任意正整数。
1637年法国数学家皮耶•费马在阅读《算术》的这个命题时,他搞了一个跨世纪、跨时空的恶作剧,他在旁边写了一段话:“将一个立方数分为两个立方数的和,一个四次方数分为两个四次方数的和,或者一般地将一个n次方数分为两个同次方数的和,这是不可能的。关于此,我确信已找到了一个真正奇妙的证明,可惜这儿的空白太小,写不下。”这就是费马猜想的由来。
在此后的350多年里,大量的数学家关注到该问题,包括欧拉、狄里赫莱、库默尔、法尔廷斯等人做出了大量有意义的工作。终于,1995年5月,美国普林斯顿出版的《数学年刊》发表了论文,困扰数学界多年的费马猜想,被英国数学家安德鲁·怀尔斯所证明。除了推动费马问题的解决之外,所创造的方法也推动了数学的发展。
二、四色问题
四色问题(即“四色猜想”)的基本内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行。1852年英国地图制图师弗朗西斯·古特里首先提出四色问题;数学家阿瑟·凯莱1872年向伦敦数学学会正式提出四色问题,于是该问题成了世界数学界关注和研究的问题。四色问题是一个可与费马猜想相媲美的难题。
在四色问题的研究过程中,不少新的数学理论随之产生,也发展了很多数学计算技巧。如将地图的着色问题化为图论问题,丰富了图论的内容。不仅如此,四色问题不仅仅是因为证明一个数学难题,更重要的是这说明计算机也能用于数学的逻辑证明。在科技飞速发展的今天,机器辅助数学证明成为了人们关注和研究的对象。
三、黎曼假设
1859年由德国数学家波恩哈德·黎曼提出的关于ζ函数ζ(s)的零点分布的猜想(即“黎曼假设”);该函数的所有非平凡零点都位于复平面上Re(s)=1/2的直线上(Re(s)表示复数s的实数部分)。德国数学家戴维·希尔伯特在第二届国际数学家大会上提出了20世纪数学家应当努力解决的23个数学问题,其中便包括黎曼假设。现今克雷数学研究所悬赏的世界七大数学难题中也包括黎曼假设。
虽然在知名度上,黎曼假设不及费马猜想,但它在数学上的重要性要远远超过后者,是数学界最重要的数学难题之一,当今数学文献中已有超过一千条数学命题以黎曼假设(或其推广形式)的成立为前提。2018年9月,英国数学家迈克尔·阿蒂亚贴出了他证明黎曼假设的预印本,但是这一证明并不成立 。
四、周氏猜测
数学猜想通常是利用观察、类比、分析、归纳等方法提出的,或者是在灵感中、直觉中闪现出来的。例如,中国数学家、语言学家周海中根据已知的梅森素数及其排列,巧妙地运用联系观察法和不完全归纳法,于1992年正式提出了梅森素数分布的重要猜想(即“周氏猜测”)。该猜想认为当2^(2^n)<p<2^(2^(n+1))时,梅森数有2^(n+1)-1个是素数。
美籍挪威数论大师、菲尔茨奖和沃尔夫奖得主阿特勒·塞尔伯格指出:“周氏猜测具有创新性,开创了富于启发性的新方法;其创新性还表现在揭示新的规律上。”由中国数学家、中科院院士张景中主编的《30年科技成就100例》一书指出:周氏猜测不仅是一项重大突破,而且具有数学之美。
五、蜂窝猜想
蜂窝猜想是由四世纪古希腊数学家佩波斯提出;蜂窝的优美形状,是自然界最有效劳动的代表。虽然蜂窝是一个三维体建筑,但每一个蜂巢都是六面柱体,而蜂蜡墙的总面积仅与蜂巢的截面有关。于是,他就此引出一个数学问题,即寻找面积最大、周长最小的平面图形。他的这一猜想称为“蜂窝猜想”,但此猜想一直没有人能证明。
直到1999年,美国科学家伊诺·黑尔才给出了蜂窝猜想的初步证明;2001年他对自己的证明再次进行了补充。自此,困扰数学界1600多年的猜想终于被证明了;所以蜂窝猜想也变成了蜂窝定理:以同等面积的区域对一个平面进行分隔,周长为最小的几何形状是蜂窝状的正六边形。
以上是几个著名数学猜想的简介;而数学猜想是猜想者运用分析、综合、演绎,尤其是类比、归纳等科学发现的思维方法,通过对数学对象和客观现象的洞察而预测新的数学事实与规律。创新性是其重要特征,没有创新,就谈不上数学猜想;创新是数学猜想的灵魂,它需要改变旧的思维方式、方法,突破固有的理论观点。数学猜想的创新性表现于揭示新的数学事实、预见新的数学规律。可见,创新性是数学猜想的一大特点,也是数学独特魅力的一种体现。
猜想在数学的发展过程中有着重要的地位。如果没有猜想,数学将寸步难行;如果没有猜想,如今这座雄伟瑰丽的数学宫殿就不会存在。可见猜想对于数学发展有着巨大的推动作用,不仅是由猜想得到结论,可以作为进一步研究的基础和出发点,而且还在于一个好的深刻的猜想往往会成为数学家们长期研究的课题,成为推动数学不断向前发展的源泉和动力。
因此可以说,数学猜想对于数学进步的作用巨大,而数学进步往往影响着一个国家的综合实力。对于数学猜想之于科学知识的作用。德国数学家卡尔·高斯有句名言:“若无某种大胆果敢的猜想,一般是不可能有知识进展的。”数学知识的进展往往会促进科学的发展,乃至唤起科学的革命。
文/苏琪(作者单位:德国莱比锡马普数学研究所)